章節連結
從網路課程 程式必修課!離散數學與演算法 來淺嚐一下沒機會在課堂上所學的離散數學與演算法。或許對撰寫程式的效能提昇會有些幫助。
課程相關資訊
[連結]:https://hiskio.com/courses/1196/lectures/133649
本篇範圍:Chapter 3
請注意:本系列文章為個人對應課程的消化吸收後,所整理出來的內容。換言之,並不一定會包含全部的課程內容,也有可能會添加其他資源來說明。
內容
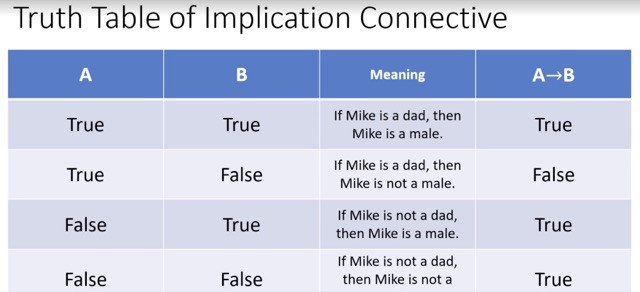
Implication ( → )
型式為 If A, then B,( 若 A 則 B )。思考時,A, B 的反面也要一同考慮
舉例:A 為 Mike 是爸爸;B 為 Mike 是男性
A 為 true, B 為 true :A → B 的意義為「若 Mike 是爸爸,那 Mike 是男性」,所以 A → B 為 true
A 為 true, B 為 false :A → B 的意義為「若 Mike 是爸爸,那 Mike 不是男性」,所以 A → B 為 false
A 為 false, B 為 true :A → B 的意義為「若 Mike 不是爸爸,那 Mike 是男性」,所以 A → B 為 true
A 為 false, B 為 false :A → B 的意義為「若 Mike 不是爸爸,那 Mike 不是男性」,所以 A → B 為 true
Take Away
A 若是錯的,那可無視 B ,A → B 結果一定是 true
A 為 true ;B 為 false ,A → B 結果才會是 false。其餘一律都是 true
B 為 true 的情況下,A → B 一定是 true

![[筆記] 程式必修課!離散數學與演算法 – 81 [筆記] 程式必修課!離散數學與演算法 – 81](https://smlpoints.com/wp-content/uploads/notes-essential-programming-discrete-math-algorithms-python-javascript-1.jpg)