[筆記] Master The Coding Interview – 1

工程師的面試中，不免俗的會遇見用各種型式來考你的演算法功力。這篇是 Udemy 上的知名課程 – Master the Coding Interview 的進修心得。目標是在這兩邊的精進後，可以自在的解決 LeetCode 上的問題。

---

課程相關資訊

[連結]：https://www.udemy.com/course/master-the-coding-interview-data-structures-algorithms/

課程對應章節：22~47

請注意：本系列文章為個人對應課程的消化吸收後，所整理出來的內容。換言之，並不一定會包含全部的課程內容，也有可能會添加其他資源來說明。

---

內容

環境設置

為了操作上的方便，可以使用 Repl.it 或是 Glot.io 來進行操作。如果你是 JavaScript 的使用者，也可以直接使用瀏覽器的 Console 工具

背景知識

1. 怎樣的 Code 會被認為是高品質的？
Readable (閱讀性) 和 Scalable (可擴展性)。前者為讓他人容易讀懂，而後者則是跟 BigO 有關聯。當你的數量級越大時，你的程式碼能不能正常運作，還是會讓使用者等待時間過就造成錯誤。

2. BigO
複雜度的表格，可以上 Big O CheatSheet 的網站查看，下方是該網頁截圖：
當 BigO 的橫軸為項目總數(n)，縱軸為操作次數。常作為代表 O(n) 為一條線型函數，操作的最大次數跟 n 有關。一般而言，我們會以 O(n) 作為標準，盡量避免產出大於 O(n) 的函式。
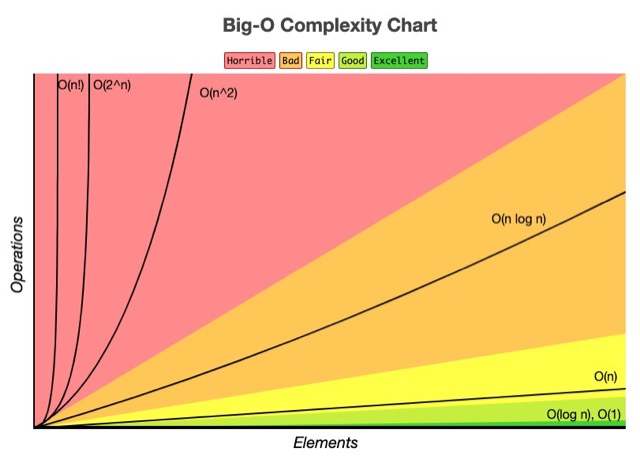
真實的 Big O 值，你需要一行行計算，但你當操作次數越發增加時，其函式的係數是可以被忽略的。
Big O 的值所呈現的，是代表整個函式執行最壞的情況。真實情況通常會在最好跟最壞之間。

3. 時間和空間複雜度

除了易讀之外，記憶體的使用量關乎 Space Complexity 而速度則是跟 Time Complexity 有關。理想情況下，自然是兩者都越有效率越好。

4. 空間複雜度計算
命名新變數、物件需要佔空間

---

小結

其實跟判斷函數極限值是相同道理的：去掉常數、次方高是主要影響者

O(1) Constant- no loops
O(log N) Logarithmic- usually searching algorithms have log n if they are sorted (Binary Search)
O(n) Linear- for loops, while loops through n items
O(n log(n)) Log Liniear- usually sorting operations
O(n^2) Quadratic-  Two nested loops
O(2^n) Exponential- recursive algorithms that solves a problem of size N
O(n!) Factorial- you are adding a loop for every element

Iterating through half a collection is still O(n)
Two separate collections: O(a * b)

---

相關文章

按讚加入粉絲團

延伸閱讀

• [筆記] 程式必修課！離散數學與演算法 – 7
• [筆記] 實作動畫 div 移入效果需注意滾軸所造成的影響
• [筆記] 程式必修課！離散數學與演算法 – 6
• [筆記] 程式必修課！離散數學與演算法 – 5
• [筆記] 程式必修課！離散數學與演算法 – 4