章節連結
- 課程相關資訊
- 內容
- Array
- Stack
- Queue
- Stack / Heap Memory
- Stack Overflow
- Garbage Collection
- Tree
- Binary Search Tree
- Binary Heaps
- Tree Traversal
- Traversal 的途徑
- LeetCode 題目
- 700. Search in a Binary Search Tree
- 100. Same Tree
- 144. Binary Tree Preorder Traversal
- 841. Keys and Rooms
- 102. Binary Tree Level Order Traversal
- 相關文章
一腳踏入軟體工程師寫 Code 的世界,不免俗地會碰上 Leetcode 的測驗,來測試你的溝通力、系統性地解決問題的能力和如何化抽象為具體。第五週的活動要進入抽象的資料結構 Stacks, Queues & Tree 實作。
課程相關資訊
[連結]:https://www.accupass.com/event/2010251353233453323900
課程對應章節:Week5 U32~U39
請注意:本系列文章為個人對應課程的消化吸收後,所整理出來的內容。換言之,並不一定會包含全部的課程內容,也有可能會添加其他資源來說明。
內容
Array
在記憶體中是連續組成,這也是和 Linked List 最大差別。在後者要查找元素,必然得從頭開始一個個遍歷。
Stack
Last In First Out ( LIFO ),一般會有 push() [將一個東西新增], pop() [將一個東西移除], peek() / top() [取出頂端的值], isFull(), isEmpty() 這幾種方法。
Queue
First In First Out ( FIFO ),一般會有 enqueue(), dequeue(), peek() / top(), isFull(), isEmpty() 這幾種方法。
不過在 JavaScript 中,其 Array 已經內建了 push(), pop(), shift(), unshift() 這四種好用的方法,僅需要搭配組合就可以當成 stack 和 queue。Stack 為 push + pop. Queue 為 push + shift
Stack / Heap Memory
Stack Memory ( 由上往下的去存放靜態變數到記憶體 ) / Heap Memory (由下往上存放動態變數到記憶體),而兩者中間的區塊就是尚未使用到的區塊。
Stack Overflow
指的是記憶體中的 Stack,表示你的程式中的靜態變數已經超出了記憶體 Stack 部分的使用量。
Garbage Collection
它會自己去猜想你的動態記憶體部分 (Heap) 是否有需要被清理掉的東西,然後幫你執行。例如 JAVA 有內建這個機制。
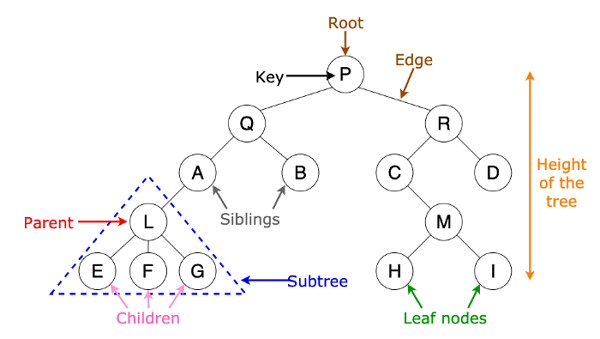
Tree
用下面圖解來說明吧:你會發現這是每一條路徑都是單向的連結,才不會有無窮迴圈的情形
在實際練習時,也可以使用視覺化工具(如:Tree 視覺化工具)
Binary Search Tree
子節點最多兩個、由左到右是由小到大的排序
Binary Heaps
子節點最多兩個、可以細分為 Min-heap 和 Max-heap。以 Min-heap 為例子,父節點一定會比下方的子節點小
Tree Traversal
為何會有 Traversal 的區別,是因為這種立體的結構,若要顯示在命令列中,那勢必得轉換成線性的狀態。這樣一來,就要決定怎樣輸出。
In-order
輸出順序是由小到大 ( 左中右 )
Pre-order
輸出順序是先 root,再左右 ( 中左右 )
Post-order
輸出順序 root 為最後 ( 左右中 )
LevelOrder
輸出順序依照階層,然後同層中為左中右的形式
Traversal 的途徑
BFS ( Breadth First Search )
廣度優先,常搭配 Queue + loop / iteration 的形式,因為具有先進先出的特質,很適合用迴圈來執行
DFS ( Depth First Search )
深度優先,常搭配 Stack + Recursion 的形式,因為可使用遞迴找到目標物,再層層堆疊輸出
LeetCode 題目
700. Search in a Binary Search Tree
連結:https://leetcode.com/problems/search-in-a-binary-search-tree/
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @param {number} val * @return {TreeNode} */ var searchBST = function(root, val) { let target = { ...root} if(target.val === val) return target if(target.val<val){ return searchBST(target.right,val) } if(target.val>val){ return searchBST(target.left,val) } return null }; |
100. Same Tree
連結:https://leetcode.com/problems/same-tree/
|
1 2 3 4 5 6 7 |
var isSameTree = function(p, q) { if(p === null && q=== null) return true if((p === null && q!== null)||(p !== null && q=== null)) return false if(p.val !== q.val) return false return isSameTree(p.left,q.left) && isSameTree(p.right, q.right) }; |
144. Binary Tree Preorder Traversal
連結:https://leetcode.com/problems/binary-tree-preorder-traversal/
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
var preorderTraversal = function(root) { let res = [] traverse(root) function traverse(node){ if(!node) return; res.push(node.val) traverse(node.left) traverse(node.right) } return res }; var preorderTraversal = function(root) { if(!root) return [] let result = [] let tempStack = [] let current = root while(current || tempStack.length){ while(current){ result.push(current.val) // 將右半的留待之後調用 tempStack.push(current.right) current = current.left } current = tempStack.pop() } return result }; |
841. Keys and Rooms
連結:https://leetcode.com/problems/keys-and-rooms/
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
var canVisitAllRooms = function(rooms) { const visitedArray = [ true , ... Array(rooms.length-1).fill(false)] const queue = [0] for(let i=0; i<queue.length; i++){ let keys = rooms[queue[i]] for(let j=0; j<keys.length;j++){ if(!visitedArray[keys[j]]){ queue.push(keys[j]) visitedArray[keys[j]] = true } } } return visitedArray.every(d=>d===true) }; var canVisitAllRooms = function(rooms) { let keyBox = [0] let keyIndex = 0 while(keyBox.length > keyIndex){ keyBox = [... new Set([... keyBox, ... rooms[keyBox[keyIndex]]])] keyIndex++ } return keyBox.length === rooms.length }; |
102. Binary Tree Level Order Traversal
連結:https://leetcode.com/problems/binary-tree-level-order-traversal/
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
// recursive with DFS var levelOrder = function(root) { if(!root) return [] const anwser = [] traverse(root,0) function traverse(node,level){ if(!node) return; anwser[level] ? anwser[level].push(node.val) : anwser[level] = [node.val] traverse(node.left, level+1) traverse(node.right, level+1) } return anwser }; |

![[筆記] AlphaCamp 不只是刷題的 Leetcode 訓練營 – 3 [筆記] AlphaCamp 不只是刷題的 Leetcode 訓練營 – 3](https://smlpoints.com/wp-content/uploads/notes-alphacamp-leetcode-training-camp-1.jpg)